发表于 | 更新于 | 分类于 | 评论数：
本文字数： 7k字 | 阅读时长 ≈ 6 分钟

动态规划

算法总体思想？

如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而提高计算效率。

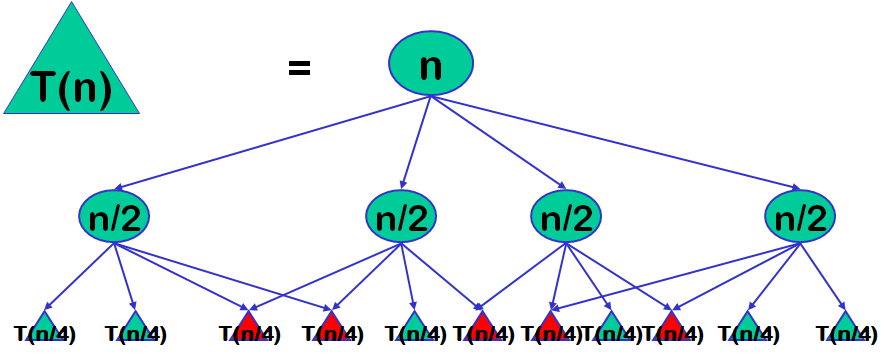
1560640223959

基本步骤（重要）

  1. 找出最优解的性质，并刻划其结构特征。
  2. 递归地定义最优值。
  3. 以自底向上的方式计算出最优值。
  4. 根据计算最优值时得到的信息，构造最优解。

矩阵连乘问题

有四个矩阵A，B，C，D，为了计算乘积ABCD，共有多少种不同的乘法顺序？

若阶数分别为：A: 50*10，B: 10*40，C: 40*30，D: 30*5。哪种乘法顺序效率最高？

答：5种。

序号 乘法顺序 乘法次数
1 (((AB)C)D) 87500
2 ((AB)(CD)) 36000
3 ((A(BC))D) 34500
4 (A((BC)D)) 16000
5 (A(B(CD))) 10500

矩阵连乘问题定义：

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。

一、找出最优解的性质，并刻划其结构特征。

特征：计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。

若先不想动态规划，使用前面前面的分治法，可得递归定义式：

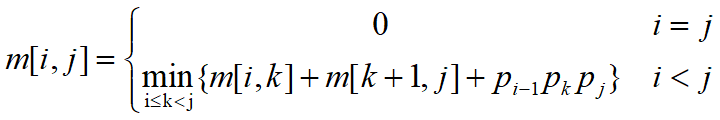
1560642284300

利用该递归定义式可以直接写出递归函数来计算m[i:j]

static int recuMatrixChain (int i, int j)
{
    if (i == j) return 0;
    int u = recuMatrixChain (i+1,j) + p[i-1]p[i]p[j];
    for (int k = i+1; k < j; k++) {
        int t = recuMatrixChain (i,k) + recuMatrixChain (k+1,j) + p[i-1]p[k]p[j];
        if (t < u) {
            u = t;
        }
    }
    return u;
}

但是该算法的复杂度如何呢？

1560642776468

递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次（子问题的重叠性质）。

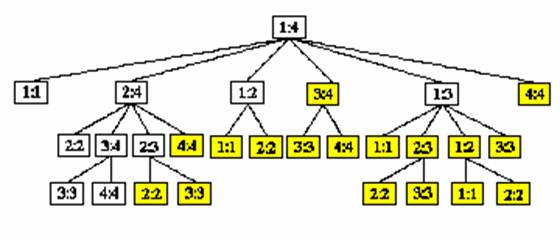
1560643003673

二、递归地定义最优值。

设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n]

当i=j时，A[i:j]=Ai，因此，m[i,i]=0，i=1,2,…,n

当i<j时，有

可以递归定义m[i,j]：

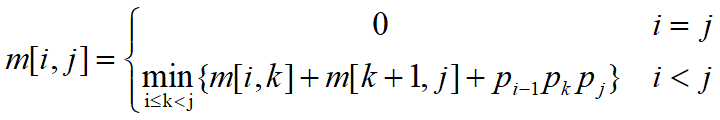
1560643530464

和上面是一样的。

三、以自底向上的方式计算出最优值。

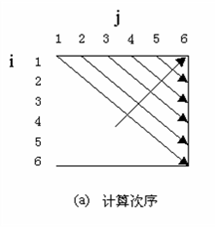
1560644456440

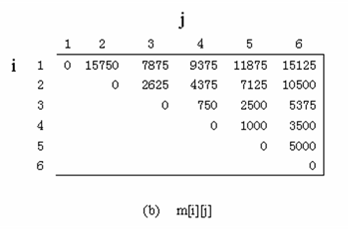
1560644525758

public static void matrixChain(int [] p, int [][] m )
{
    int n=p.length-1;
    for (int i = 1; i <= n; i++) m[i][i] = 0;
    for (int r = 2; r <= n; r++){
        for (int i = 1; i <= n - r+1; i++) {
            int j=i+r-1;
            m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];
            for (int k = i+1; k < j; k++) {
                int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (t < m[i][j]) {
                    m[i][j] = t;
                }
            }
        }
    }
}

四、根据计算最优值时得到的信息，构造最优解。

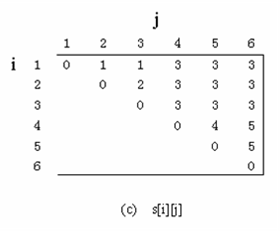
1560644471185

public static void matrixChain(int [] p, int [][] m )
{
    int n=p.length-1;
    for (int i = 1; i <= n; i++) m[i][i] = 0;
    for (int r = 2; r <= n; r++){
        for (int i = 1; i <= n - r+1; i++) {
            int j=i+r-1;
            m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];
            s[i][j] = i;
            for (int k = i+1; k < j; k++) {
                int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (t < m[i][j]) {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }
}

动态规划算法的基本要素

一、最优子结构

矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。

在分析问题的最优子结构性质时，所用的方法具有普遍性：首先假设由问题的最优解导出的子问题的解不是最优的，然后再设法说明在这个假设下可构造出比原问题最优解更好的解，从而导致矛盾。

利用问题的最优子结构性质，以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提。

注意：同一个问题可以有多种方式刻划它的最优子结构，有些表示方法的求解速度更快（空间占用小，问题的维度低）

二、重叠子问题

递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称为子问题的重叠性质。

动态规划算法，对每一个子问题只解一次，而后将其解保存在一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。

通常不同的子问题个数随问题的大小呈多项式增长。因此用动态规划算法只需要多项式时间，从而获得较高的解题效率。

三、备忘录方法

备忘录方法的控制结构与直接递归方法的控制结构相同，区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看，避免了相同子问题的重复求解。

m<-0
private static int lookupChain(int i, int j)
{
    if (m[i][j] > 0) return m[i][j];
    if (i == j) return 0;
    else{
        int u = lookupChain(i+1,j) + p[i-1]*p[i]*p[j];
        s[i][j] = i;
        for (int k = i+1; k < j; k++) {
        int t = lookupChain(i,k) + lookupChain(k+1,j) + p[i-1]*p[k]*p[j];
        if (t < u) {
            u = t;
            s[i][j] = k;
        }
        m[i][j] = u;
        return u;
    }
}

最长单调递增子序列

设计一个O(n^2)时间的算法，找出由n个数组成的序列的最长单调递增子序列。

设序列为a[0:n-1]，记b[i]：以a[i]为结尾元素的最长递增子序列的长度。

则序列a的最长递增子序列长度为

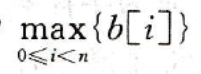
1560645732752

如何求b[i]？

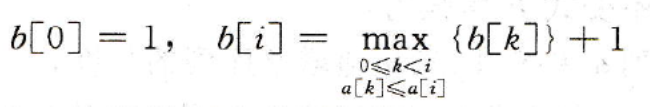
1560645762252

1560645775860

最长公共子序列

1560645858051

给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}，找出X和Y的最长公共子序列。

设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ，则

1)若xm=yn，
则zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列。

2)若xm≠yn，
则Z是
Xm-1和Y的最长公共子序列，X和Yn-1的最长公共子序列，
中较长的序列。

子问题的递归结构

由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录序列的最长公共子序列的长度。其中， Xi={x1,x2,…,xi}；Yj={y1,y2,…,yj}。当i=0或j=0时，空序列是Xi和Yj的最长公共子序列。故此时c[i][j]=0。其他情况下，由最优子结构性质可建立递归关系如下：

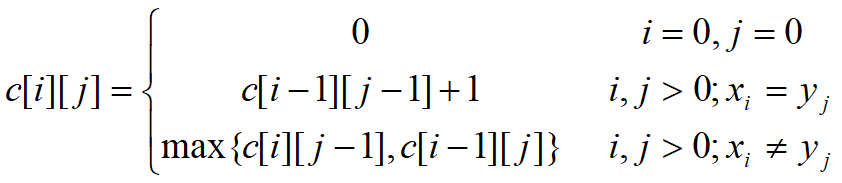
1560645994913

计算最优值、最优解

1560646077487

凸多边形最优三角剖分

表示具有n条边的凸多边形:用多边形顶点的逆时针序列表示凸多边形，即P={v0,v1,…,vn-1}。

若vi与vj是多边形上不相邻的2个顶点，则线段vivj称为多边形的一条弦。弦将多边形分割成2个多边形{vi,vi+1,…,vj}和{vj,vj+1,…vi}。

多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。

给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得即该三角剖分中诸三角形上权之和为最小。

最优子结构性质

事实上，若凸(n+1)边形的最优三角剖分T包含三角形，1≤k≤n-1，则T的权为3个部分权的和：三角形的权，子多边形和的权之和。可以断言，由T所确定的这2个子多边形的三角剖分也是最优的。

因为若有或的更小权的三角剖分将导致T不是最优三角剖分的矛盾。

多边形游戏问题

多边形游戏是一个单人玩的游戏，开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值，每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。

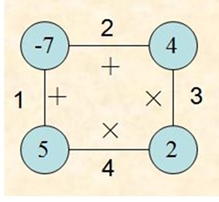
1560647037626

游戏第1步，将一条边删除。

随后n-1步按以下方式操作：

(1)选择一条边E以及由E连接着的2个顶点V1和V2；

(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。

最后，所有边都被删除，游戏结束。游戏的得分就是所剩顶点上的整数值。

1560647143255

问题：对于给定的多边形，计算最高得分。

1560647361233

1560647378493

1560647402856

图像压缩

电路布线

流水作业调度

0-1背包问题

最优二叉搜索树

发表于 | 评论数：
本文字数： 459字 | 阅读时长 ≈ 1 分钟

软件测试

date: 2019-06-15 13:59:00

常见的接口测试类型？

HTTP（get、post）、WebService（get、post）（wsdl）、socket（少见）

工具的选用

Jmeter（基于Java实现的）

Firefox的插件httprequester

在线工具 http://www.atool.arg/httptest.php

postman（一个插件）

soapui

loadrunner

例子

http类型的接口测试，老黄历接口：https://v.juhe.cn/laohuangli/d

data={“key”:”sdsfasdafdsafsafdsa”,data:”2019-03-23”}

聚合数据网站还有其它接口

app界面元素
  1. 各种栏（状态栏、导航栏、标签栏、工具栏）
  2. 内容视图（列表、卡片、集合视图、图片、文本）
  3. 控制元素（页面控制器、分段式控件、滑动开关、选择器、文本框、按钮、进度条、刷新视图、调节器）
  4. 临时视图（警示视图、操作列表、模态视图、toast）

发表于 | 分类于 | 评论数：
本文字数： 3.8k字 | 阅读时长 ≈ 3 分钟

第一章

1-1 说明下面的方法swap为什么无法交换实际参数的值？
1
2
3
4
5
6
public static void swap(int x,int y) 
{
	int temp=x;
	x=y;
	y=temp;
}

方法参数传的是值（基本数据类型），不是引用，方法调用结束后，参数x、y出栈。

1-2 说明下面的两个方法头是否有不同的签名，为什么？

(1) public int fff(int i,int j,int k)
(2) public float fff(int i,int j,int k)

相同，只要方法名和参数列表相同，他们的方法签名就相同，他们都是fff+int i,int j,int k。

1-4 求下列函数的渐进表达式。
阅读全文 »

发表于 | 更新于 | 分类于 | 评论数：
本文字数： 6.7k字 | 阅读时长 ≈ 6 分钟

分治法

计算阶乘n!

设计递归函数，计算n!的值，其中n>0。

1
2
3
4
int factorial(int n){
    if(n==1) return 1;
    else return factorial(n-1)*n;
}

Fibonacci数列

Hanoi塔

假定n-1个盘子的转移算法已确定，对n个圆盘的问题：

​ 第1步：把A上面的n-1个圆盘经C转移到B上

​ 第2步：把A最下面的一个圆盘移到C上

​ 第3步：把B上的n-1圆盘经A转移到C上

转移完毕。

算法分析：令h(n)表示n个圆盘所需要的转移盘次，则算法复杂度为？

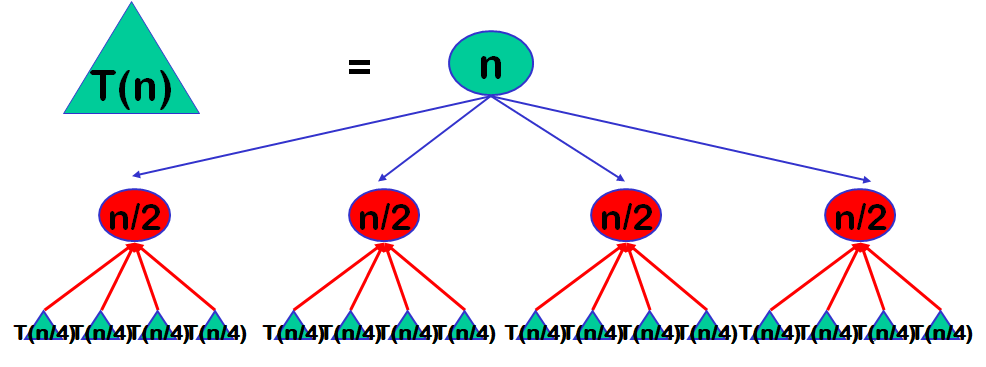
分治算法总体思想

  1. 将求解的较大规模的问题分割成k个更小规模的子问题。对这k个子问题分别求解。

    比如上面的factorial函数，将n规模的任务缩小为n-1规模的任务。任务规模不一定缩小为n-1，也可能是n/2（如：折半查找）等等。

  2. 如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。

  3. 将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

    1560520502208

阅读全文 »

发表于 | 更新于 | 分类于 | 评论数：
本文字数： 511字 | 阅读时长 ≈ 1 分钟

第一章

程序 = ？

数据结构+算法

算法的四个特性？

输入、输出、有穷、确定

好的算法？

正确性、可读性、健壮性、高效率和低存储量需求

算法复杂度排序？

复杂度按数量级递增排列依次为：常数阶O(1)、对数阶O(logn)、线性阶O(n)、线性对数阶O(nlogn)、平方阶O($n^{2}$)、立方阶O($n^{3}$)、…、k次方阶O($n^{k}$)、指数阶O($2^{n}$)、阶乘阶($n!$)。

算法复杂度分析中的四个符号是？分别代表什么？

Ω O θ o
≥ 渐渐下界 ≤ 渐进上界 ＝ ＜
阅读全文 »

发表于 | 更新于 | 评论数：
本文字数： 2.9k字 | 阅读时长 ≈ 3 分钟

创建新文章(post)？

1
$ hexo new "My New Post"

开启本地服务器？

1
$ hexo server

生成静态文件？

1
$ hexo generate

部署到远程网站？

1
$ hexo deploy

必须注意，在hexo d的时候，不是把所有文件上传一遍，它会检查本地部署日志文件，然后再根据修改情况进行相应地部署。

所以，如果你在其它地方更新了远程仓库的某个文件，本地没有进行更新，你调试的时候可能会出错，你还奇了怪了。

记住：以本地仓库为主，别在远程更新文件！

hexo网页中出现阿拉伯文？

设置语言时出现了问题，把zh_cn改成zh-CN试试。

给文章添加标签？

把文章添加标签只需在文章的顶部标题下方添加tags字段，即可自动创建标签名并归入对应的标签中
举个栗子：

1
2
3
4
5
title: 标签测试文章标题
tags: 
  - 标签1
  - 标签2
  ...

给文章分类？

把文章归入分类只需在文章的顶部标题下方添加categories字段，即可自动创建分类名并加入对应的分类中
举个栗子：

1
2
title: 分类测试文章标题
categories: 分类名

设置侧边栏（sidebar）？

打开主题配置文件找到sidebar字段。

头像设置？

打开主题配置文件找到Sidebar Avatar字段（侧边栏阿凡达）。

1
2
# Sidebar Avatar
avatar: /images/header.jpg

这是头像的路径，只需把你的头像命名为header.jpg（随便命名）放入themes/next/source/images中，将avatar的路径名改成你的头像名就OK啦！

在主页不想要展示一个文章所有内容，添加阅读全文按钮？

如果你想让你的文章只显示一部分，多余的可以点击阅读全文来查看，那么你需要在你的文章中添加

1
<!--more-->

其后面的部分就不会显示了，只能点击阅读全文才能看。

文章基本设置：

1
2
3
4
5
6
7
8
9
10
11
12
---
title: CentOS7下Tomcat启动慢的原因及解决方案
date: 2017-12-02 21:01:24
comments: true #是否可评论
toc: true #是否显示文章目录
categories: "云服务器" #分类
    - 分类1
    - 分类2
tags:   #标签
	- 标签1
	- 标签2
---

图片？

写文章时，hexo的图片文件都放在了与md文件同名的文件夹下（md文件和文件夹是分离的）。

然而，生成public静态文件时，图片文件却与index.html文件在同一个文件夹。

在md文件中采用相对路径引用图片，生成的html也会采用相对路径来引用图片，但此时图片和html是在同一个文件夹啊！所以页面当然不能正常显示图片了。

解决方法：到这个仓库去，https://github.com/xcodebuild/hexo-asset-image.git

安装该插件以后，还得到\node_modules\hexo-asset-image去改index.js脚本文件。因为它的有错误！

比如我发现这么个错误：

1
2
// var endPos = link.lastIndexOf('.'); //获取最后一个点的位置，不就是.io吗？也说不定啊，文件名可以允许有点啊。比如xxx.xxx.jpg，这里显得不严谨！所以后面切子串的时候错了！
var endPos = getPosition(link, '/', 7);

改完这个后，再在typora设置：

1560780948049

现在我可以在typora上可视化的插入图片进行编写md文件了。

不用写那么麻烦的官方标签了，比如：

1
{% asset_img 这是一个新的博客的图片.jpg 这是一个新的博客的图片的说明 %}

这样的标签在typora上无法渲染，在GitHub上也无法渲染，因为它是hexo独有的，不推荐。

卸载该插件：

1
npm uninstall hexo-asset-image

安装该插件：

1
npm install hexo-asset-image --save

latex数学公式？

注意，使用latex公式时，要用两个$$符号，不是一个，不然在网页端解析会出现问题。

以两个美元符号开始一行的话，可能会被忽略掉！如下：

1
$$64n^{2} = n1^{2}$$，解得n1=8n。

md文件中敲再多连续的空格，到了网页上都只会显示一个空格。于是就想着将md文件中的连续的四个空格替换为：

1
&nbsp;&nbsp;&nbsp;&nbsp;

怎么实现呢？用nodejs 替换文件中所有图片的url

参考上面的文章。把它写好后，在hexo g开始后，马上替换掉md文件中符合要求的内容，这样就不用每次都选中，然后ctrl+h进行替换了。

思路有了，但目前还没去做，现在我只是在notepad++中进行CTRL+H。

除了空格需要替换，数学表达式中的星号*也需要转义，因为md文件中星号可能被用于加粗字体。

貌似左括号“[”右括号“]”也需要转义。

Hexo 如何引入自定义 js 文件

Hexo 中静态文件放在主题文件夹中，即

1
your_project/themes/<theme_name>/source

在这个文件夹中会有 js, css, img 等文件夹，没有的话可以自己创建，将自定义的 js 放到其中，在 markdown 文章中直接引用即可。

1
<script type="text/javascript" src="/js/test.js"></script>

可以不用在markdown文章中引用，在

1
\themes\next\layout\_layout.swig

中引用也可以。

主题目录下的source文件夹中的文件部署的时候，会直接放到仓库中。

下载pdf.js稳定版，解压后放在主题目录下的source文件夹中，部署，

输入： https://chiuinmeng.github.io/pdf.js/web/viewer.html

就可查看pdf。

https://chiuinmeng.github.io/pdf.js/web/viewer.html?file=https://chiuinmeng.github.io/2019/06/17/%E3%80%8A%E7%AE%97%E6%B3%95%E8%AE%BE%E8%AE%A1%E4%B8%8E%E5%88%86%E6%9E%90%E3%80%8B4.%20%E8%B4%AA%E5%BF%83%E6%B3%95/%E8%B4%AA%E5%BF%83%E6%B3%95.pdf

便可查看其它pdf

hexo中应该放pdf吗？

不推荐！！！pdf是二进制文件，不是文本文件，所以对于搜索引擎不友好，无法直接搜索pdf中的文字信息。