第一章
1-1 说明下面的方法swap为什么无法交换实际参数的值?
1 | public static void swap(int x,int y) |
方法参数传的是值(基本数据类型),不是引用,方法调用结束后,参数x、y出栈。
1-2 说明下面的两个方法头是否有不同的签名,为什么?
(1) public int fff(int i,int j,int k)
(2) public float fff(int i,int j,int k)
相同,只要方法名和参数列表相同,他们的方法签名就相同,他们都是fff+int i,int j,int k。
1-4 求下列函数的渐进表达式。
1-5 说明0(1)和O(2)的区别。
O(1)和O(2)差别仅在于其中的常数因子,根据渐进上界记号O的定义可知,O(1)=O(2)。
1-6 按照渐进阶从低到高的顺序排列以下表达式:$4n^2, logn, 3^n,20n,2,n^{2/3}$。又n!应该排在哪一位?
n>=1时,有
n>=7时,有
1-7(1) 假设某算法在输入规模为n时的计算时间为T(n)=32^n。在某台计算机上实现并完成该算法的时间为t秒。现有另外一台计算机,其运行速度为第一台计算机的64倍,那么在这台新机器上用同一算法在t秒内能解输入规模为多大的问题?
设能解输入规模为n’的问题,则,解得n’=n+6。
1-7(2) 若上述算法的计算时间改进为T(n)=n^2,其余条件不变,则在新机器上用t秒时间能解输入规模多大的问题?
有,解得n’=8n。
1-7(3) 若上述算法的计算时间进一步改进为T(n)=8,其余条件不变,那么在新机器上用t秒时间能解输入规模多大的问题?
由于T(n)=常数,因此算法可解任意规模的问题。
1-8 硬件产商XYZ公司宣称他们最新研制的微处理器运行速度为其竞争对手ABC公司同类产品的100倍。对于计算复杂性分别为n, n^2, n^3, 和n!的各算法,若用ABC公司的计算机能在1小时内能解输入规模为n的问题,那么用XYZ公司的计算机在1小时内分别能解输入规模为多大的问题?
n’=100n
n’^2=100n^2得到n’=10n
n’^3=100n^3得到n’=4.64n
n’!=100n!得到n’<n+log100=n+6.64
1-9 对于下列各组函数f(n)和g(n),确定f(n)=O(g(n))或f(n)=Ω(g(n))或f(n)=θ(g(n)),并简述理由。
(1) f(n)=, g(n)=logn+5 // θ
(2) f(n)=, g(n)= // n>=8时,O
(3) f(n)=n, g(n)= // Ω
(4) f(n)=nlogn+n, g(n)=logn // Ω
(5) f(n)=10, g(n)=log10 // θ
(6) f(n)=, g(n)=logn // Ω
(7) f(n)=, g(n)=100 // Ω
(8) f(n)=, g(n)= // O
知识点:
f(n)的阶不高于g(n)的阶:f(n)=O(g(n));
f(n)的阶不低于g(n)的阶:f(n)=Ω(g(n));
f(n)与g(n)同阶:f(n)=θ(g(n))
1-10 证明:n!=o(n^n)
1-11 证明:如果一个算法在平均情况下的计算时间复杂度为θ(f(n)),则该算法在最坏情况下所需的计算时间为Ω(f(n))。
1 | Tavg(N)=IeDn∑P(I)T(N,I) |
因此,Tmax(N)=Ω(Tavg(N))=Ω(θ(f(n)))=Ω(f(n))
第二章 分治法
2-2 下面的7个算法与本章的二分搜索算法binarySearch略有不同。请判断这7个算法的正确性。如果算法不正确,请说明产生错误的原因;如果算法正确,请给出算法的正确性证明。

(1)与主教材中的算法binarySearch相比,数组段左、右游标left和right的调整不正确,导致陷入死循环

(2)与主教材中的算法binarySearch相比,数组段左、右游标left和right的调整不正确,导致当x=a[n-1]时返回错误。

(3)与正确算法binarySearch5相比,数组段左、右游标left和right的调整不正确,导致当x=a[n-1]时返回错误。

(4)与正确算法binarySearch5相比,数组段左、右游标left和right的调整不正确,导致陷入死循环。

(5)算法正确,且当数组中有重复元素时,返回满足条件的最右元素。

(6)与正确算法binarySearch5相比,数组段左、右游标left和right的调整不正确,导致当x=a[n-1]时返回错误。

(7)与正确算法binarySearch5相比,数组段左、右游标left和right的调整不正确,导致当x=a[0]时陷入死循环。
2-3 设a[0:n-1]是已排好序的数组。请改写二分搜索算法,使得当搜索元素x不在数组中时,返回小于x的最大元素位置i和大于x的最小元素位置j。当搜索元素在数组中时,i和j相同,均为x在数组中的位置。
分析与解答:改写二分搜索算法如下:
public static boolean binarySearch(int []a, int x, int left, int right, int []ind)
{
int middle;
while ( left <= right ) {
middle = (left + right)/2;
if (x == a[middle]) { ind[0]=ind[1]=middle; return true;}
if (x > a[middle]) left = middle + 1;
else right = middle -1;
}
nd[0] = right; ind[1]=left;
return false;
}
返回的ind[1]是小于x的最大元素位置,ind[0]是大于x的最小元素的位置。
2-4 给定两个整数u和v,他们分别有m和n位数字,且m<=n。用通常的乘法求uv的值需要O(mn)时间。可以将u和v均看作是有n位数字的大整数,用本章介绍的分治法,在$O(n^{log3})$时间内计算uv的值。当m比n小得多时,用这种方法就显得效率不够高,试设计一个算法,在上述情况下用$O(nm^{log(3/2)})$时间求出uv的值。
当m比n小的多,就把n分成n/m段,所以就相当于一共有n/m次,计算m位乘法运算。
m位乘法运算的复杂度为:
总的复杂度为:
2-5 在用分治法求两个n位大整数u和v的乘积时,将u和v都分割成长度位n/3位的3段。证明可以用5次n/3位整数的乘法求得uv的值。按此思想设计一个求两个大整数乘法的分治算法,并分析算法的计算复杂性。(提示:n位的大整数除以一个常数k可以在θ(n)时间内完成。符号θ所隐含的常数可能依赖于k。)
按照此算法计算大整数乘积需要5次n/3位整数乘法。大整数分割、移位、加减法和数乘运算时间位O(n)。设T(n)是算法所需的计算时间,则:
2-6 对任何非零偶数n,总可以找到奇数m和正整数k,使得n=m×2^k。为了求出两个n阶矩阵的乘积,可以把一个n阶矩阵分成m×m个子矩阵,每个子矩阵有
将n阶矩阵分块为m×m的矩阵。用传统方法求2个m阶矩阵的乘积需要计算次2个矩阵的乘积。用Strassen矩阵乘法计算2个矩阵的乘积需要的计算时间为,因此算法的计算时间为
2-7 设$P(x)=a{0}+a{1}x+…+a_{d}x^{d}$是一个d次多项式。假设已有一算法能在O(i)时间内计算一个i次多项式与一个1次多项式的乘积,以及一个算法能在O(ilogi)时间内计算两个i次多项式的乘积。对于任意给定的d个整数n1,n2,…,nd,用分治法设计一个有效算法,计算出满足P(n1)=P(n2)=…=P(nd)=0且最高次项系数为1的d次多项式P(x),并分析算法的效率。

2-8 设n个不同的整数排好序后存于T [ 0 : n-1 ] 中。若存在一个下标i ,0 < i < n , 使得T[i] = i , 设计一个有效算法找到这个下标。要求算法在最坏情况下的计算时间为O(logn)。
提示:二分,T[i]与i比较

2-15给定数组a[0:n-1],试设计一个算法,在最坏情况下用$\left \lceil 3n/2-2 \right \rceil $次比较找出a[0:n-1]中元素的最大值和最小值。
若从头到尾一次遍历。最坏比较2(n-1)次(不满足题意),最好比较n-1次,平均(3n-3)/2。
1 | int a[n]; |
方法1:每一次都取最边上的两个比较,大的与max比,小的与min比,这样每轮比较3次,共n/2轮。第一轮只需比较1次,故总次数:3n/2-2。
2-16 给定数组a[0:n-1],试设计一个算法,在最坏情况下用$n+\left \lceil logn \right \rceil -2$次比较找出a[0:n-1]中元素的最大值和次大值。
算法思想:用分治法求最大值和次大值,首先将问题划分, 即将划分成长度相等的两个序列, 递归求出左边的最大值次大值, 再求出右边的的最大值次大值, 比较左右两边, 最后得出问题的解。
最大值一定在左边或右边最大值中的一个,次大值的选取还得比较一次,总共得经过两次比较。
这个结果O(n),题目要求的也属于O(n)。
2-25 在算法select中,输入元素被划分为5个一组,如果将他们划分为7个一组,该算法仍然是线性时间算法吗?划分为3个一组又怎样?

2-26 试说明如何修改快速排序算法,使它在最坏情况下的计算时间为O(nlogn)。


2-27 给定由n个互不相同的数组成的集合以及正整数k≤n,试设计一个O(n)时间算法,找出S中最接近S的中位数的k个数。
提示:找最小的k个数(线性时间选择)
1)找出S的中位数median;
2)计算T={|x-median|∣x∈S}
3)找出T的第k小元素y;
4)根据y找出所要的解{x∈S∣|x-median|≤y}

2-28 设X[0:n-1]和Y[0:n-1]为两个数组,每个数组中有n个已排好序的数。试设计一个O(logn)时间的算法,找出X和Y的2n个数的中位数。
提示:看到O(logn),你应该想到折半查找,所以会涉及到分块,分块后该问题解的分析有些麻烦,别太想当然了。





第三章 动态规划
3-1 设计一个O(n^2)时间的算法,找出由n个数组成的序列的最长单调递增子序列。


3-2 将习题3-1中算法的计算时间减至O(nlogn)。(提示:一个长度为i的候选子序列的最后一个元素至少与一个长度为i-1的候选子序列的最后一个元素一样大。通过指向输出序列中元素的指针来维持候选子序列)。



3-3
3-4
3-5
3-6
第四章 贪心算法
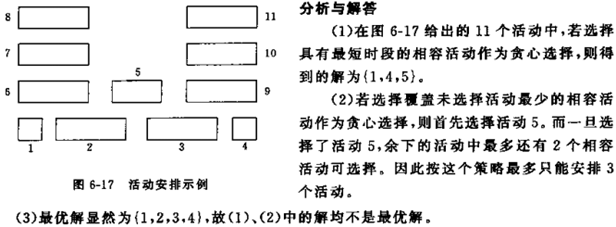
4-1 在活动安排问题中, 还可以有其他的贪心选择方案, 但并不能保证产生最优解。给出一个例子, 说明若选择具有最短时段的相容活动作为贪心选择, 得不到最优解;若择覆盖未选择活动最少的相容活动作为贪心选择, 也得不到最优解。
4-2 证明背包问题具有贪心选择性质。
4-3 若在0-1背包问题中,各物品依重量递增排列时,其价值恰好依递减序排列。对这个特殊的0 -1 背包问题,设计一个有效算法找出最优解,并说明算法的正确性。


4-6 字符a-h出现的频率恰好是前8 个Fibonacci数,它们的哈夫曼编码是什么?将结果推广到n个字符的频率恰好是前n个Fibonacci 数的情形。
| a | 1111111 |
|---|---|
| b | 1111110 |
| c | 111110 |
| d | 11110 |
| e | 1110 |
| f | 110 |
| g | 10 |
| h | 0 |
4-12 试设计一个构造图G生成树的算法,使得构造出的生成树的边的最大权值达到最小。
可以证明,图G的最小生成树即为满足题意的生成树。
假设T,T’分别为图G的最小生成树及边的最大权值达到最小值的生成树。v,v’分别为它们的最大权边。假如w(v)>w(v’),则将v从T删除之后,T变为两个连同的分支,此时,一定有T’的边v1连同这两个分支,否则T’将是不连通的。从而将v1加入到T中构成一新的生成树T’’=T-v+v1。且有w(v1)<w(v’)<w(v),从而w(T”)=w(T-v+v1)<w(T)。这与T为最小生成树矛盾。
证毕。据此利用prim算法或者Kruskal算法算得G的最小生成树即可。
Prim算法 O(n2)
首先置 S={1},然后,只要S是V的真子集,就作如下的贪心选择:选取满足条件i∈S,j∈V-S,且c[i][j]最小的边,将顶点j添加到S中。 这个过程一直进行到S=V时为止。在这个过程中选取到的所有边恰好构成G的一棵最小生成树。 在上述Prim算法中,还应当考虑如何有效地找出满足条件i∈S, j∈V-S,且权c[i][j]最小的边(i,j)。实现这个目的的较简单的办法是设置2个数组closest和lowcost。在Prim算法执行过程中,先找出V-S中使lowcost值最小的顶点j,然后根据数组closest选取边(j,closest[j]),最后将j添加到S中,并对closest和lowcost作必要的修改。
Kruskal算法 O(eloge)
首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小到大排序。然后从第一条边开始,依边权递增的顺序查看每一条边,并按下述方法连接2个不同的连通分支:当查看到第k条边(v,w)时,如果端点v和w分别是当前2个不同的连通分支T1和T2中的顶点时,就用边(v,w)将T1和T2连接成一个连通分支,然后继续查看第k+1条边;如果端点v和w在当前的同一个连通分支中,就直接再查看第k+1条边。这个过程一直进行到只剩下一个连通分支时为止。
第五章 回溯法
第六章 分支限界法
补充
独立任务最优调度问题